Question
has anyone used the 'Linear regression: Predicted Y' function ? pls help me to understand how it work?
I have created the below metrics. However, I am not sure whether it is correct? and why predicted data keeps on changing?
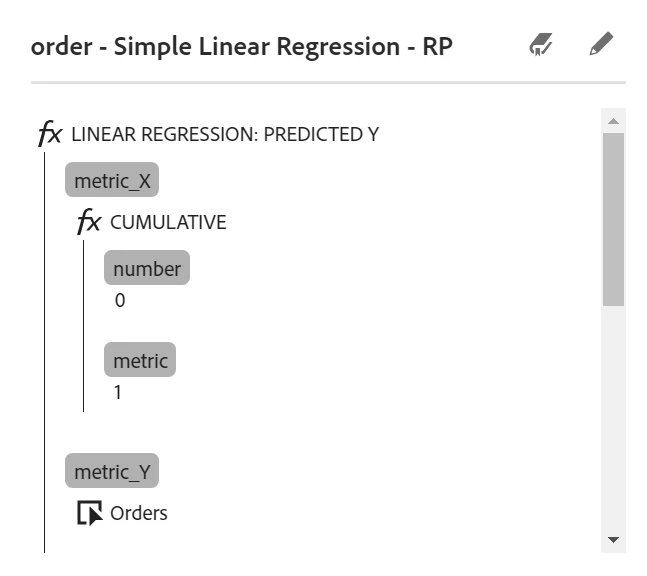
I have created the below metrics. However, I am not sure whether it is correct? and why predicted data keeps on changing?

Enter your E-mail address. We'll send you an e-mail with instructions to reset your password.